SHORT INTRODUCTION TO ELECTRO ACOUSTIC THEORY
Electroacoustic effects are result of coupling between acoustic and electric fields. Debye realized 70 years ago that in the presence of longitudinal sound wave, any differences in the effective mass or friction coefficient between anions and cations would result in different displacement amplitudes. In turn, this difference in displacement would create an alternating electric potential between points within the solution. Indeed, this phenomenon is measurable and can yield useful information about the properties of ions. It is usually referred to as an “Ion Vibration Potential”. It was used for measuring sizes of ions in 60th.
However, the main application field of electroacoustic effects is in characterization of heterogeneous systems that contain two or more phase. The first electroacoustic theory was developed for porous materials saturated with liquid in 1944 by Frenkel . He created theory of this electroacoustic effect keeping in mind wet soils and other geological formations. That is why he assigned name “electro-seismic” to this phenomenon. We use this effect now for studying zeta potential of porous materials with DT-330 Zeta Potential probe.
Further studies extended electroacoustic measurements to dispersions and emulsions. Detail historical review of all developments on the field of electroacoustics can be found in our book Dukhin, A.S. and Goetz, J.P. “Characterization of Liquids, Nano- and Microparticulates, and Porous Bodies using Ultrasound”, Edition 3, Elsevier, 571 pages, 765 references, (2017).
Here we present just one very useful expression for “Colloid Vibration Current” (CVI) derived by Shilov et al (see book by Dukhin and Goetz) using a well-known Onsager reciprocal relationship for Smoluchowski type electrokinetic theory:
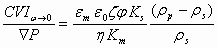
where ε is dielectric permittivity, η is viscosity, ρ is density, φ is volume fraction, K is conductivity, ζ is zeta potential. Index p corresponds to particle, m to media, s to the system in whole.
This equation is very useful for estimating trend of electroacoustic measurement depending on various parameters. It is valid quantitatively for submicron particles with sizes under 300 nm with thin double layer and negligible surface conductivity. Double layers must be not overlapped, which restricts somewhat volume fraction for a given particle size.
